3  Molecular Mechanics in Molecular Modelling

Molecular modelling started with the idea that molecular geometry, energy, and other molecular properties could be calculated from models (that are influenced by basic forces).

A molecule - hence - is a system of particles (i.e., atoms) connected by springs (i.e., bonds). This molecule is free to rotate, vibrate, and adopt a favorable conformation in space as a result of the inter- and intramolecular forces acting upon it.

3.1 Structure, Topology, Motion, Functions, and Potential Energy

This section aims to illustrate how different energy functions can influence the behavior of particles in a system.

3.1.1 Case #1

A Simple System to Consider

The potential and kinetic energy \(E_p\) and \(E_k\) respectively in this system is given by:

\[\begin{align} E_p &= E_p(\vec{x}) = \sum_{i}f_i(x, y, z) \\ E_k &= \frac{1}{2} \cdot (m_1v_1^2 + m_2v_2^2) \end{align}\]

Where \(\vec{x}\) is the system and \(f_i(x, y, z)\) a function that calculates the potential energy for each particle in the system (i.e., each atom). Hence, we can say that:

\[\begin{equation} E_{tot} = E_p + E_k \end{equation}\]

Where \(E_{tot}\) is the total energy of the system.

Since \(r\) represents the distance between both molecules, therefore \(E_p(r) = 0\).

\[\begin{equation} \vec{F} = \frac{\partial E_p(\vec{x})}{\partial \vec{x}} \end{equation}\]

The force1 \(\vec{F}\) on the system is denoted via the above equation.

Since \(E_p(r) = 0\) in the first figure, it follows that \(F(r) = 0\).

3.1.2 Case #2

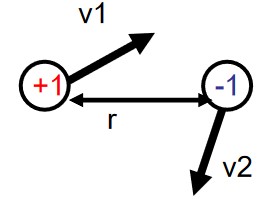
A System with Two Charged Molecules

Here, the charge \(V_{ele}\) and the potential energy \(E_p(r)\) is given via the following equations:

\[\begin{align} V_{ele}(r) &= \frac{1}{4\pi \epsilon_0} \cdot \frac{q_1}{r} \\ E_p(r) &= \frac{1}{4\pi \epsilon_0} \cdot \frac{q_1q_2}{r} \end{align}\]

Some important considerations to think about include the variables and the parameters of the system.

3.1.3 Case #3

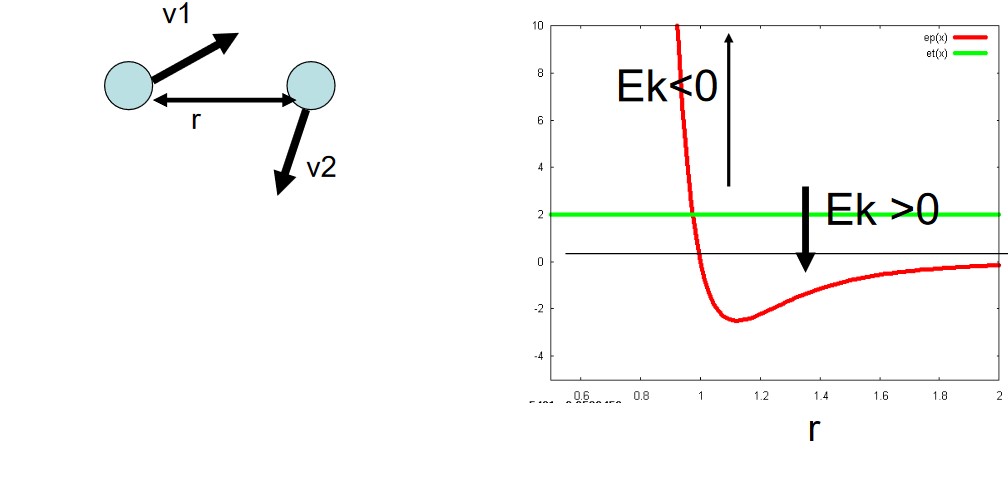
A System with Two Molecules and their Energy Graph

In this system, we let:

\[\begin{equation} E_p(r) = 4\epsilon\left[\left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^6\right] \end{equation}\]

In this system, we also note that \(E_p(r) = 0\) when \(r = \sigma\) and that \(\displaystyle E_p(\sqrt[6]{2}\sigma) = -\epsilon\).

Do also consider the variables and parameters in this system (and whether or not both particles in this system can move freely).

3.1.4 Case #4

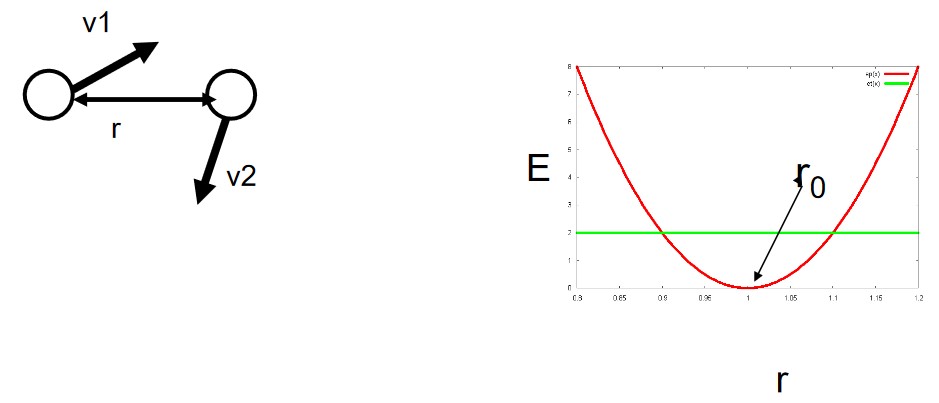
A System with Two Molecules and their Energy Graph

Here, we define the system’s potential energy \(E_p\) as:

\[\begin{equation} E_p(r) = \frac{1}{2}k(r - r_0)^2 \end{equation}\]

While the energy graph for this system appears to be that of bonding, it is still important to consider the variables and the parameters of the system.

We can also further decompose the above equation to its spatial components \(x\), \(y\), and \(z\) and say that:

\[\begin{equation} E_p(r) = \frac{1}{2}k(x - x_0)^2 + \frac{1}{2}k(y - y_0)^2 + \frac{1}{2}k(z - z_0)^2 \end{equation}\]

In this sub-case, the system appears to be a lattice. However, are the particles still movable?

3.2 Professor Mu’s Current Works

As of the time of writing, professor Mu’s lab is currently focused on the following topics:

  1. Amyloidogenic protein / peptide aggregation and misfolding
  2. DNA-DNA, DNA-ions, and DNA-protein interactions
  3. Drug-protein interaction and drug candidate screening
  4. Peptide-membrane interactions.

For more information on professor Mu’s current research topics, do visit his lab’s homepage.

  1. Note that \(\vec{F}\) is caused by a change in potential energy, not by potential energy itself!↩︎